Funciones par e impar
En el estudio de las funciones reales de variable real, si consideramos el punto , nos interesa el comportamiento de cuando se toma el . Puede suceder que obtenga el mismo resultado que , en cuyo caso se trata de una función par. También puede suceder que para , se obtenga de modo que el resultado no es el mismo que el de , en cuyo caso se trata de una función impar. En el aspecto geométrico la no variación de al cambiar a , revela simetría de la gráfica de respecto al eje Y. La variación de a al reemplazar por , indica simetría respecto al origen de coordenadas. Entre las funciones reales hay funciones pares, impares y que no asumen ninguno de los casos mencionados. Por ejemplo , no es par ni impar, ya que no podemos definir esta función para números reales negativos.[1]
También una función par se define en álgebra como f(x),y una función impar se define como f(-x).
Las funciones pares e impares son usadas en muchas áreas del análisis matemático, especialmente en la teoría de las series de potencias y series de Fourier.
Funciones pares
[editar]
Una función par es una función que satisface la relación y si y -x están en el dominio de la función.
Desde un punto de vista geométrico, la gráfica de una función par es simétrica con respecto al eje y, lo que quiere decir que su gráfica no se altera luego de una reflexión sobre el eje y.
Ejemplos de funciones pares son la función valor absoluto f(X)= |x|, las funciones elementales f(x)=x2, f(X)= x4, f(X)= cosx; una función hiperbólica f(X)= cosh(x), todas definidas en ℝ, la ampliación f(x)=ln|x| de ln, con dominio ℝ-{0}; la función f(x)= 1/|x|, reflexión parcial, con eje Ox, de f(x) =1/x en su subdominio <-∞; o>.
Definición formal
[editar]El término función par suele referirse a una clase especial de funciones de variable real: una función es una función par si para se cumple la siguiente relación:
La definición anterior puede generalizarse a funciones sobre dominios más generales. Si A es un conjunto con cierta estructura algebraica en la que existan inversos aditivos (por ejemplo, los números complejos C), una función par sería toda función:
que cumpla:
La definición de función par presupone que si entonces necesariamente , de no ser así no se podría definir .
Ejercicio de ejemplo
[editar]La función:
es par ya que para cualquier valor de x se cumple:
Comprobando que la función es par.
Si x=2, entonces:
Funciones impares
[editar]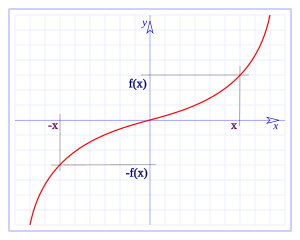
Una función impar es cualquier función que satisface la relación:
para todo en el dominio de .
Desde un punto de vista geométrico, una función impar posee una simetría rotacional con respecto al origen de coordenadas, lo que quiere decir que su gráfica no se altera luego de una rotación de 180 grados alrededor del origen.
Ejemplos de funciones impares son x, x3, seno(x), sinh(x), y la erf (x).
Ejemplo
[editar]La función:
- , cuya gráfica es la hipérbola simétrica respecto al origen
J es impar, ya que:
en este caso la función no está definida en el punto .
Si vemos la función:
Podemos ver que se cumple:
Y esta función si pasa por el punto (0,0).
Características
[editar]La paridad de una función no implica que sea diferenciable o continua.
Propiedades
[editar]- La única función que es tanto par como impar es la función constante Cero definida por f(x) = 0, para cualquier valor real de x.
- La suma de una función par y una impar no necesariamente es par o impar.
- La suma de dos funciones par es una función par, y todo múltiplo de una función par es una función par. En resumen es función par, donde f y g son funciones pares, σ y τ están en ℝ.
- La suma de dos funciones impares es una función impar, y todo múltiplo constante de una función impar es una función impar. O sea es función impar, donde f y g son funciones impares, δ y κ están en ℝ.
- El producto de dos funciones pares es una función par.
- El producto de dos funciones impares es una función par.
- El producto de una función par y una función impar es una función impar.
- El cociente de dos funciones pares es una función par.
- El cociente de dos funciones impares es una función par.
- El cociente de una función par y una función impar es una función impar.
- La derivada de una función par es una función impar, en los valores donde exista la derivada.[2]
- La derivada de una función impar es una función par.
- La composición de dos funciones pares es una función par, y la composición de dos funciones impares es una función impar.
- La composición de una función par y una función impar es una función par.
- La composición de toda función con una función par es par (pero no viceversa).
- Toda función definida sobre toda la línea real puede descomponerse en la suma de una función par y una impar:
- La integral de una función impar entre -A y +A es cero (donde A es finito o infinito, y la función no posee ninguna asíntota vertical entre -A y A).
- La integral de una función par entre -A y +A es el doble de la integral entre 0 y +A (donde A es finito, y la función no posee ninguna asíntota vertical entre -A y A).
Series
[editar]- La serie de Maclaurin de una función par se compone solo de términos con potencias pares.
- La serie de Maclaurin de una función impar se compone solo de términos con potencias impares.
- La serie de Fourier de una función par periódica solo incluye términos cosenos.
- La serie de Fourier de una función impar periódica solo incluye términos senos.
Véase también
[editar]Referencias
[editar]Enlaces externos
[editar]- Weisstein, Eric W. «Función par». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Función impar». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.




































